5 Optimisation

The underlying design of NanoCap and the generalisation of point sets and forcefields, allows for a great deal of flexibility in optimisation routines. The same optimisation routine that is used to minimised the total dual lattice energy can be used to optimise the carbon lattice using a force field such as EDIP. 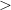Currently three methods of minimising the total energy are implemented and can be selected in either the Calculations– $>$ Dual Lattice or Calculations– $>$ Carbon Lattice options as shown in Fig. 8:

$\includegraphics[scale= 0.5]{../../screens/nanocap_dual_lattice_options_win.png}$ $\includegraphics[scale= 0.5]{../../screens/nanocap_carbon_lattice_options_win.png}$

Figure 8: NanoCap Optimisation options are shown for both the dual lattice and carbon lattice option windows.

These options include the number of minimisation steps and the tolerance used to determine convergence. A brief description of each of the optimisers is given below:

L-BFGS
The most robust optimiser in NanoCap is the Limited-memory Broyden–Fletcher–Goldfarb–Shanno method (LBFGS). This routine requires forces which are used to iteratively update an estimate of the Hessian matrix, which in turn is used to define new directions along which to perform line searches. NanoCap uses the the LBFGS method as implemented in the scipy.optimise libraries (http://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.fmin_l_bfgs_b.html) which have a theoretical basis in the following publications:
A Limited Memory Algorithm for Bound Constrained Optimization R. H. Byrd, P. Lu and J. Nocedal. (1995), SIAM Journal on Scientific and Statistical Computing, 16, 5, pp. 1190-1208.
L-BFGS-B: Algorithm 778: L-BFGS-B, FORTRAN routines for large scale bound constrained optimization C. Zhu, R. H. Byrd and J. Nocedal. (1997), ACM Transactions on Mathematical Software, 23, 4, pp. 550 - 560.
L-BFGS-B: Remark on Algorithm 778: L-BFGS-B, FORTRAN routines for large scale bound constrained optimization J.L. Morales and J. Nocedal. (2011), ACM Transactions on Mathematical Software, 38, 1.
SD
The steepest descent (SD) method minimises energy by simply following the direction of force (i.e. the negative gradient of the potential field). The step size per iteration is determined by the current magnitude of force. The SD method is useful when visualising the optimisation process.
SIMPLEX
The simplex method is an optimisation routine which does not require the calculation of forces. As such is the only optimiser that works with the Scaled Topology force field. The implementation in NanoCap again comes from the scipy.optimise libraries which implement algorithms presented in the following publications:
A Simplex Method for Function Minimization Nelder, J.A. and Mead, R. The Computer Journal, 7, pp. 308-313
Direct Search Methods: Once Scorned, Now Respectable Wright, M.H. Numerical Analysis 1995, Proceedings of the 1995 Dundee Biennial Conference in Numerical Analysis pp. 191-208