Nanotubes

2.2 Nanotubes

To construct a nanotube the user has the option for either a finite-length nanotube or one that is periodic along the axial direction.

$\includegraphics[scale= 0.5]{../../screens/nanocap_nanotube_init_finite_win.png}$ $\includegraphics[scale= 0.5]{../../screens/nanocap_nanotube_init_periodic_win.png}$

Figure 3: Nanotube construction options

Finite tubes

Finite tubes are constructed as close to a user defined length as possible. This is done by constructing strips of basis points along the chiral vector (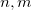 $n,m$ ):

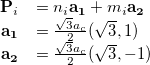$\begin{equation*} \begin{array}{rl} \boldsymbol {\mathrm{P}}_ i & = n_ i\boldsymbol {\mathrm{a_1}} + m_ i\boldsymbol {\mathrm{a_2}}\\ \boldsymbol {\mathrm{a_1}} & = \tfrac {\sqrt {3}a_ c}{2} (\sqrt {3}, 1)\\ \boldsymbol {\mathrm{a_2}} & = \tfrac {\sqrt {3}a_ c}{2} (\sqrt {3}, -1)\\ \end{array}\end{equation*}$

where 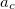$a_ c$ is the carbon bond length of 1.421 . The incremented values ( 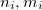$n_ i,m_ i$ ) range from (0,0) to ( 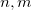$n,m$ ) and depends on:

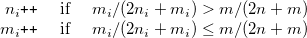$\begin{equation*} \begin{array}{rl} n_ i\verb!++! & \mbox{ if~ ~ $m_ i/( 2n_ i+m_ i)>m/( 2n+m)$} \\ m_ i\verb!++! & \mbox{ if~ ~ $m_ i/( 2n_ i+m_ i)\leq m/( 2n+m)$} \\ \end{array}\end{equation*}$

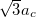After each new row of points, the origin is translated in the $z$ direction by $\sqrt {3}a_ c$ . The current distance along the nanotube axis is then compared against the user defined length to determine if another strip should be added. The user defined length is inputted in the Calculations– $>$ Input options.

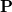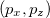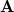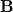At each basis point $\boldsymbol {\mathrm{P}}$ at position $(p_ x,p_ z)$ , the positions of the carbon atoms ( $\boldsymbol {\mathrm{A}}$ and $\boldsymbol {\mathrm{B}}$ ) and dual lattice points ( 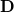$\boldsymbol {\mathrm{D}}$ ) are given by:

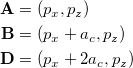$\begin{equation*} \begin{split} \boldsymbol {\mathrm{A}} & = (p_ x , p_ z)\\ \boldsymbol {\mathrm{B}} & = (p_ x +a_ c , p_ z)\\ \boldsymbol {\mathrm{D}} & = (p_ x + 2a_ c , p_ z) \end{split}\end{equation*}$

Periodic tubes

Periodic tubes are constructed using a user defined number of unit cells in the z direction. The periodic length 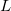$L$ of a nanotube of chirality ( 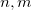$n,m$ ) with $u$ unit cells is given by:

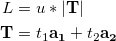$\begin{equation*} \begin{split} L & = u*|\boldsymbol {\mathrm{T}}|\\ \boldsymbol {\mathrm{T}} & = t_1\boldsymbol {\mathrm{a_1}} + t_2\boldsymbol {\mathrm{a_2}} \end{split}\end{equation*}$

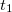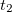where the coefficients $t_1$ and $t_2$ have no common divisors except for unity and are given by:

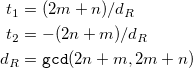$\begin{equation*} \begin{split} t_1 & = (2m + n)/ d_{R} \\ t_2 & = -(2n + m)/ d_{R} \\ d_{R} & = \texttt{gcd}(2n+m, 2m+n) \end{split}\end{equation*}$

During construction, the carbon atoms and dual lattice points are generated as for the finite tubes, the only difference being the replacement of the user-defined length with the periodic length. After construction, any points surpassing the periodic length are removed.

The number of unit cells for a periodic nanotube can be found in the Calculations– $>$ Input options.

The resultant periodic length after construction can be found in the Information options tab. This will be required by simulation software if the nanotube is to be used in a periodic simulation.