Dual Lattice Force Fields

4.1 Dual Lattice Force Fields

Currently, only one force field is implemented to optimise a structure’s dual lattice - labelled: The Thomson Problem. The total energy of a system of 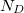$N_ D$ dual lattice points is given by the sum of pair interaction energies:

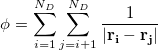$\begin{equation*} \displaystyle \phi = \sum _{i=1}^{N_{D}}\sum _{j=i+1}^{N_{D}}\frac{1}{| \boldsymbol {\mathrm{r_ i}}-\boldsymbol {\mathrm{r_ j}}| } \end{equation*}$

where $\boldsymbol {\mathrm{r}}$ denotes the position vector of each point. When the dual lattice belongs to a fullerene, the full system is included in the loop of pair interactions. For a capped nanotube however, there is restriction to the points included in the force field calculation. A cutoff length is introduced along the nanotube beyond which points are exclude from the force evaluation. This is required to ensure a uniform arrangement of points in the capped region and reduce the concentration of points in the apex of the cap. This cutoff length is automatically determined based upon the density of points in the nanotube but can be set manually in the options described in Section 2.3